Piyush, born on 10th Feb, 1967, Aquarian belongs to a middle class family in Dadri, Near Noida, elder son of Dr. Devender Kumar Goel and mother Ravikanta. He is Diploma Mechanical Engineering passed in the year 1987, Diploma in Material Management, Diploma in Vastu Shastra and Diploma in Business Management. creative, believe in God too much, believe in Love & Friendship.
This Theorem applies in Two Conditions:
- The Triangle must be Right-Angled.
- Its Sides are in A.P. Series.
We Have:
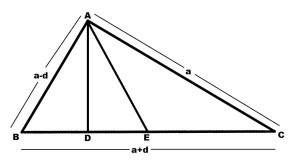
- ∆ABC is Right-Angled
- AD is Altitude
- AE is Median i.e. E is the midpoint of BC
Proof:
(a+d)2 = a2 + (a-d)2
(a+d)2 -(a-d)2 = a2
a2 + d2 + 2ad – a2 – d2 + 2ad = a2
4ad = a2
a(a-4d) = 0
a – 4d = 0 (as a ≠ 0)
a = 4d (———-eqn. 1)
In ∆ABD
AB2 = BD2 + AD2
(a – d)2 = BD2 + AD2
(a – d)2 = {(a + d)/2 – DE}2 + AD2 (———-eqn. 2)
In ∆ACD
AC2 = DC2 + AD2
a2 = DC2 + AD2
a2 = {(a + d)/2 + DE}2 + AD2 (———-eqn. 3)
From eqn. 2 & 3, we get
(a – d)2 – a2 = {(a + d)/2 – DE}2 + AD2 – {(a + d)/2 + DE}2 – AD2
(a – d +a )(a – d – a) = {(a+d)/2 – DE + (a+d)/2 + DE}{(a+d)/2 – DE – (a+d)/2 – DE}
(2a – d)(-d) = (a + d)(-2DE)
(2a – d)(d) = (a + d)(2DE)
So, 2DE = (2a – d)d/(a+d)
From eqn. 1, we get
2DE = (2*4d – d)d/(4d + d)
2DE = 7d2/5d
DE = 7d/10 = (4d + 3d)/10
But, AB = a –d = 4d – d = 3d & AC = a = 4d
Putting these values, we get
DE = (AC + AB)/10 (Hence Proved)
Devang Vibhakar is the Founder and Editor of www.SpeakBindas.com. He has interviewed more than 350 people. His effort was recognized by Limca Book of Records, twice. He has been to Scotland as well as Germany as part of vocational & cultural exchange programs and has compiled five books so far. He's passionate about bringing forth interesting stories & interviews of entrepreneurs to avid readers of SpeakBindas. He can be reached 